四则运算是我们平时使用地最频繁的操作之一,由于实在是太过底层,我们很少去考虑去自己实现这一过程。在这里,我将使用 lisp,通过实现这几个基本过程来构造出一个能够处理基本算术运算的解释器。
题外话
关于 lisp
刚开始学习 lisp 的时候,受某人的影响一度成为了一个 lisp 吹,就是狂热宗教分子那种感觉, 虽然现在这种感觉已经慢慢冷却,但总体来讲,各种客观因素都表明 lisp 确实是一门值得去学习的语言。
lisp 使用 S表达式 来书写语法,不少人都可以写出一些 lisp 程序,让它接受一段 S表达式, 并将它处理成你想得到的新表达式(eval-apply)。也就是连在程序运行时改变程序本身都能够做到。
也得益于这种语法,语法解析变得尤其简单,比如说很多语言中不能被定义的变量名、 不能被绑定的值都可以让你随便使用(有些你只能在 DrRacket 里玩),举个例子:
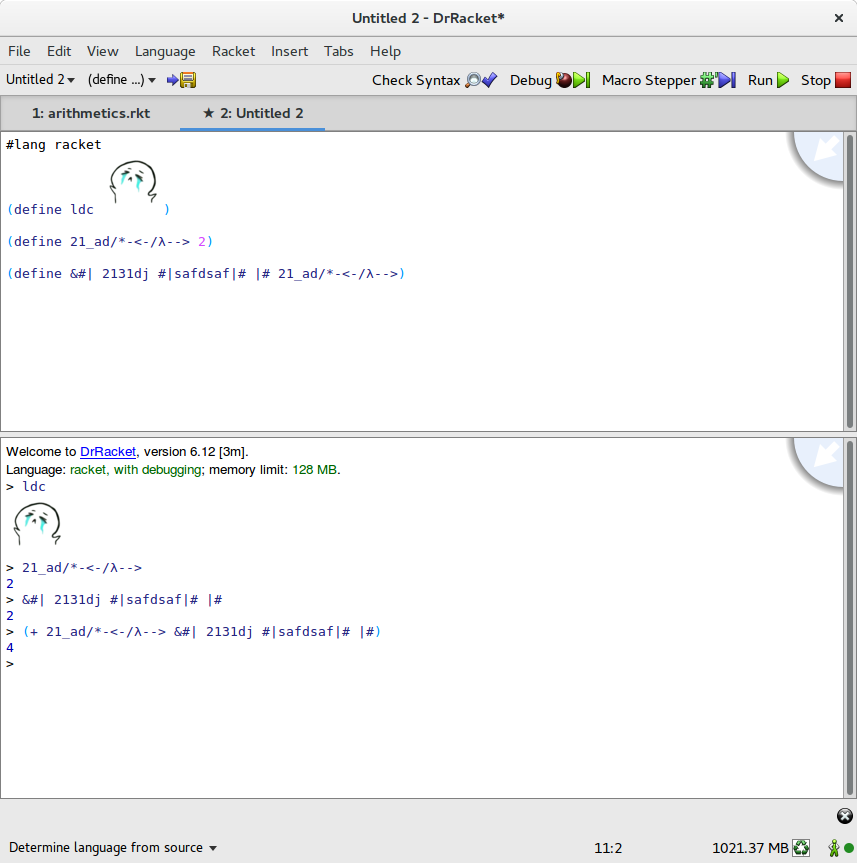
目标
- 算术运算
- 实现一个计算器
工具
由于 racket 用起来不错,所以是今天的主角就是她了,IDE 就用 DrRacket。
racket 允许你使用圆括号 () 方括号 [] 以及花括号 {} 来书写你的表达式,
唯一的要求就是一个开括号要匹配上它对应的闭括号。
你可以在 DrRacket 中用快捷键
C-\来快速插入一个 λ 符号、C-d快速展开 interactoin 面板、c-e快速展开代码编辑面板、F5或C-r重新执行你的代码。 你可以非常方便地使用 TeX 中的宏,输入完成后使用快捷键M-\即可。
你可以通过访问 http://racket-lang.org/ 进行免费下载。
基本算术的实现
我之前并没有接触过 lisp 怎么办?
这里提供一些基本认知以帮助你快速入门:
所谓 S表达式,其实是一种非常简单的树结构,比如 ‘(+ (- 3 2) (* 3 4)) ,对应的结构是:
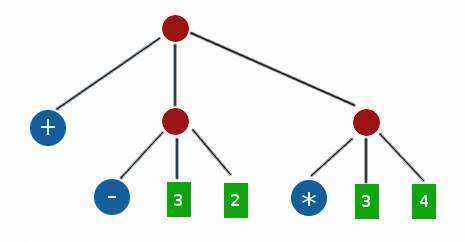
然后就是今天要用到的过程:
`(define id exp)` ; 将一个 id 绑定为 exp 的求值结果。
`(if test then else)` ; 如果 test 通过,那么执行 then 语句块,否则执行 else 语句块。
`(cond (test exp) ...)` ; 你可以把 cond 当成 if 的语法糖,也可以反过来。
`(lambda (arg ...) exp)` ; 返回一个具体的过程(函数)。
`(let ((v e) ...) exp)` ; 将 v 绑定为 e 的求值结果,然后就可以在 exp 中使用。
`(bitewise-and a b)` ; 按位与。
`(bitewise-ior a b)` ; 按位或。
`(bitewise-xor a b)` ; 按位异或。
`(bitewise-not a)` ; 按位否。
`(bitewise-bit-field a start end)` ; 截取二进制中的指定位长。
`(arithmetic-shift a n)` ; 对 a 进行位移操作,n 大于 0 时左移,小于 0 时右移。
`(integer-length a)` ; 获取二进制的位长。因为位运算的函数名实在太长,我给它们换了个皮方便使用:
(define ∧ bitwise-and)
(define ∨ bitwise-ior)
(define ¬ bitwise-not)
(define ⊕ bitwise-xor)
(define ⋯ bitwise-bit-field)你需要先熟悉一下这些过程的使用方法才能够继续往下阅读。
开始
首先实现加法,最常见的一种加法运算就是使用位运算,因为该方法在处理负数时利用了符号位会溢出的技巧, 由于 racket 中的符号位不会溢出,所以这种实现不太适合在这里使用。
这里提供一下实现与思路,有兴趣的人可以自行尝试,首先模拟一下 1 位二进制的加法:
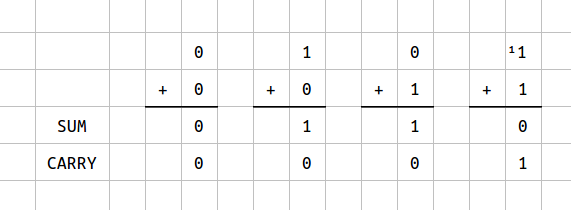
对照一下[真值表][truth-table],可以看到 SUM 与 XOR 的逻辑一样,而 CARRY 又与 AND 的逻辑一样:
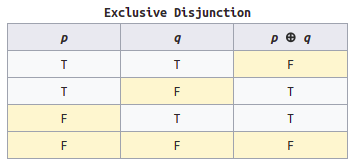
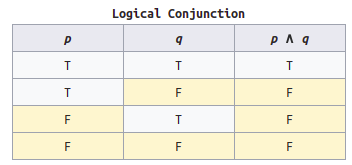
具体实现:
(define add
(λ (a b)
(let ([sum (bitwise-xor a b)]
[carry
(arithmetic-shift
(bitwise-and a b) 1)])
(cond [(zero? carry) sum]
[else (add sum carry)]))))另一种方法
由于 racket 的数字符号位是动态自增的,在使用上面那种方式在处理负数时麻烦多多, 那还有什么办法可以实现加法呢?皮亚诺公理是个不错的选择,先来看下其中的三条定义:
- 0 是一个自然数
- 对于每一个自然数 $a$,都有一个后继自然数 $S(a)$
- 0 不是任何数的后继数
那么回到问题的核心,两个数相加说到底不过是要去不断地寻找被加数的后继数而已。
为此,我们需要一个函数,它能够使任意给定数 + 1。
停一下,在继续看下去之前你需要了解一下什么是补码, 具体来说就是将二进制数进行取相反位后再加 1 即等于这个数的相反数(他们肯定是故意设计成这个样子的):
$-a \Leftrightarrow \neg a + 1$
基于这个特性,-1 在计算机中的二进制表示为所有可用位都是 1:
$\dots 0 \ 0 \ 0 \ 1 \ \Rightarrow \ +1$
$\dots 1 \ 1 \ 1 \ 1 \ \Rightarrow \ -1$
你是不是想到了什么,你大概知道我要在这里使用什么魔法了吧:
- 可以用 $a \wedge 1$ 来获取一个二进制数的第 1 位
- 当第 1 位为 0 时把它变成 1 即可实现
a + 1
即:
$(a \wedge 1 = 0) \models (a ∨ 1 = a + 1)$
不仅如此,我们还可以使用 $a \wedge -2$ 使第一位变成 0:
$(a \wedge 1 = 1) \models (a \wedge -2 = a - 1)$
通过简单的位移也能实现
-1+,由于文章中没有任何需要用到-1+操作的地方,所以这里 pass 掉。
以上就足以支撑我们写代码所需要的逻辑了,下面是具体实现:
;; simple add 1
(define 1+
(λ (x)
(letrec
([enough?
(lambda (x) (= (bitwise-and x 1) 0))] ; 判断第一位是否为 0
[loop
(lambda (x)
(cond
[(enough? x) ; 如果是 0
(bitwise-ior x 1)] ; 对其 +1
[else ; 否则则需要进位
(arithmetic-shift ; 将找到的返回值左移 1 位
(loop (arithmetic-shift x -1)) ; 将这个数字右移 1 位继续递归,直到找到 0 为止
1)]))])
(cond
[(= x -1) 0] ; 不直接返回就会发生不可描述的事情
[else (loop x)]))))你可以去测试一下这段程序的正确性,这里不再多作验证。
我们可以基于这个 1+ 函数来定义一些小工具:
;; 左移
(define ⟨ arithmetic-shift)
;; 右移
(define ⟩ (λ (n m) (arithmetic-shift n (2comp m))))
;; 二补码
(define 2comp (λ (x) (1+ (¬ x))))
;; 获取二进制的符号位
(define gs
(λ (x)
(let* ([start (integer-length x)]
[end (1+ start)])
(⋯ x start end))))
;; 是负数?
(define negative?
(λ (x)
(not (zero? (gs x)))))
;; 是 0 ?
(define zero? (λ (x) (= x 0)))
;; 是正数?
(define positive?
(λ (x)
(cond
[(zero? x) #f]
[(zero? (gs x))])))加法
加法是将两个自然数映射到另一个自然数的函数,它被递归地定义为:
\[\begin{aligned} a + 0 &= a \\ a + S(b) &= S(a + b) \\ a + 4 &= S(S(S(S(a + 0)))) \end{aligned}\]实现:
(define add
(λ (a b)
(letrec
([loop ; 如果代码被执行,则 b 一定为正数
(λ (a n) ; a 为被加数 n 为累加子
(cond
[(= n b) a] ; 如果 n 达到跳出的条件则 a 就是所得结果
[else ; 否则
(1+ (loop a (1+ n)))]))]) ; a + S(b) = S(a + b)
(cond
[(not (negative? b)) ; 如果 b 是非负数
(loop a 0)] ; 则可以直接进行求值
[(not (negative? a)) ; 如果 a 是非负数
(add b a)] ; 基于交换律,a + b ⇔ b + a
[else ; ¬¬(negative? b) ∧ ¬¬(negative? b)
(2comp (add (2comp a) (2comp b)))])))) ; 基于分配律,(-a) + (-b) ⇔ -(a + b)你可以自行改成尾调用的版本,这里为了与公式一致不再进行修改
减法
因为我找来找去都找不到对于减法的定义,所以这里我就 xjb 写一下。。。
减法也是同样的道理,显然负数并不是一个自然数,可是也显然我们能够在数轴上找到任意一个负数的后继数, 所以这里需要稍微修改一下公理以满足我们用于减法的需求:
- 0 是一个整数
- 对于每一个整数 $n$,都有一个后继整数 $S(n)$
- 0 不是任何正整数的后继数
- 0 是所有负整数的后继数
我们还没有定义减法是什么,因为减法实际上是在找被加数的前继数,所以在这里用加上一个负数来表示减法, 那么我们就可以通过加法来定义减法了:
\[\begin{aligned} b - a &= -a + b \\ -a + 0 &= -a \\ -a + S(b) &= S(-a + b) \\ -a + 4 &= S(S(S(S(-a + 0)))) \end{aligned}\]万事俱备,现在可以写代码了:
(define sub (λ (a b) (add (2comp b) a)))没错,因为我们的加法已经很完美了,因为我们的减法是完全基于加法的,所以才可能这样做。
乘法
同样,乘法是将两个自然数映射到另一个自然数的函数。给定加法,乘法将递归定义为:
\[\begin{aligned} a \times 0 &= 0 \\ a \times 1 &= a \\ a \times S(b) &= a + (a \times b) \\ a \times 4 &= a + (a + (a + (a + (a \times 1)))) \end{aligned}\](define mul
(λ (a b)
(letrec
([loop
(λ (x n)
(cond
[(= n b) x]
[else
(loop (add x a) (1+ n))]))])
(cond
[(not (negative? b))
(loop a 1)]
[(not (negative? a))
(mul b a)]
[else
(mul (2comp a) (2comp b))]))))跟加法差不多,这里就不过多废话。
除法
这里我找不到除法的定义,所以只好把乘法的公式反向一下:
\[\begin{aligned} a \div 0 &= \text{undefined} \\ 0 \div a &= 0 \\ b \div a &= S((b - a) \div a) \\ 9 \div 3 &= S((9 - 3) \div 3) \\ &= S(S((6 - 3) \div 3)) \\ &= S(S(S((3 - 3) \div 3))) \\ &= S(S(S(0 \div 3))) \\ &= S(S(S(0))) \end{aligned}\](define div
(λ (a b)
(letrec
([pa? (positive? a)]
[pb? (positive? b)]
[loop
(λ (x n)
(let ([v (sub x b)]) ; 这里将 (sub a b) 绑定为 v 以减少重复计算
(cond
[(negative? v) n]
[else
(loop v (1+ n))])))])
(cond
[(zero? a) 0]
[(zero? b) (error "dividends can not be 0")] ; 0 不能当除数
[pa? (cond
[pb? (loop a 0)] ; pa? ∧ pb?
[else ; pa? ∧ ¬ps?
(2comp (div a (2comp b)))])]
[pb? (2comp (div (2comp a) b))] ; ¬pa? ∧ pb?
[else ; ¬pa? ∧ ¬pb?
(div (2comp a) (2comp b))]))))参数的拓展
一个二元运算符只能拥有两个参数,由于我们的加法实际上是一个函数,一个函数实际上是可以拥有多个参数的,
所以我们可以这样写代码: (+ 1 2 3 4 5) ,原理可以参考链表:
cons
我们都知道基本数据类型与复合数据类型,在面向对象语言中我们可以把任何对象都叫做复合数据类型; 而在 lisp 中,复合数据类型是由基本数据类型通过某种方式加以组合形成的数据类型。
当有人想你展示一门新语言,一般来说要注意三点:
- 构成语言的基本元素有哪些?
- 组合的方法是什么?
- 抽象的方法是什么?
而 cons 就是我们在 lisp 中构造复合对象的基本方式。
cons 单元是一个存放了两个地址的内存空间,并把第一个空间称作 car,第二个空间称作 cdr,
假如我输入 (cons 1 2) 则会返回一个复合数据对象,它同时描述了这个数据中的 1 和 2:
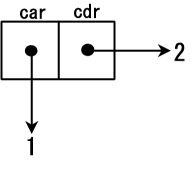
在这里,我只将 1 和 2 这两个数字组合在了一起,实际上,cons 的真正强大之处在于,
它能够将任何数据组合在一起,比如 (cons 3 (cons 1 2)):
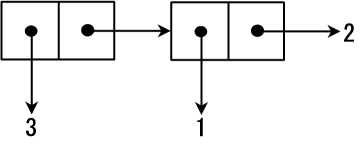
组合对象的方式有很多种,因此就有必要建立一些统一的约定:car 用于存放特定的值,
cdr 部分用于存储后续的序列,当这个序列数据中再没有其他元素时,会使用一个特殊的标记来表示结束,
(cons 1 (cons 2 (cons 3 '()))):
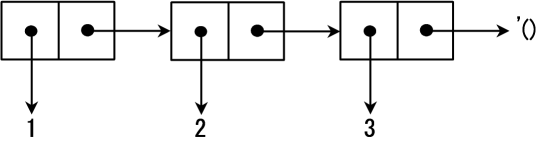
lisp 提供了一个快速创建链表的函数 list,(cons 1 (cons 2 '())) 和 (list 1 2) 是等价的。
实际上,lisp 中的链表正是使用这种方式构建出来的,链表只是 lisp 用来表示序列数据的一个约定而已。
我们可以利用词法闭包的特性来简单地实现一下 cons car cdr:
(define cons
(λ (x y)
(λ (z)
(cond [(= z 1) x]
[(= z 2) y]))))
(define car
(λ (p) (p 1)))
(define cdr
(λ (p) (p 2)))你可以做一些模型代换来理解它们。
然而有一种更广为人知的方法,这种技术被称为邱奇序对:
(define cons
(λ (x y) (λ (s) (s x y))))
(define car
(λ (c) (c (λ (x y) x))))
(define cdr
(λ (c) (c (λ (x y) y))))回到正题,λ 的第一个括号描述了这个函数需要被多少个参数调用,这里存在着一种特殊的写法:
(λ (a . b) ...) ; 注意 `a . b` 之间的空格,不然 `.` 就成了变量名的一部分而不是序对的意思了。
((λ (a . b) a) 1 2 3 4) ; => 1
((λ (a . b) b) 1 2 3 4) ; => '(2 3 4)a . b 的意思是,这个函数最少可以被 1 个参数调用,最多可以被无限个参数调用,
而所有参数都会以链表的方式被传入,a 代表了链表的 car 部分,b 代表了链表的 cdr 部分。
不要把它和其他语言中对链表的模式匹配相混淆了。
那么多个参数的加减乘除都可以实现了:
;; abstract
(define arith-loop
(λ (fun)
(letrec
([loop
(λ (acc . l)
(cond
[(null? l) acc]
[else (fun acc (apply loop l))]))])
loop)))
(define + (arith-loop add))
(define - (arith-loop sub))
(define × (arith-loop mul))
(define ÷ (arith-loop div))一个计算器
通过上面对于数据组合的介绍,你大概知道为什么 lisp 会有代码即数据这个概念了吧, 因为你可以用 cons 来构建任意的 S表达式,然后用 car 和 cdr 提取出其中的任意 S表达式。 既然如此,能不能够写一段程序,它能够解析我们的 S表达式,然后对它进行求值。
当我们输入 (+ 1 (* 2 3) 3 (/ 30 5) (+ 2 3)) 这段表达式时,lisp 会对这段代码进行解析并求值。
如果时在程序以外的地方得到一个字符串 “(+ 1 (* 2 3) 3 (/ 30 5) (+ 2 3))”,如何让 lisp 识别该字符串?
符号
在开始之前先介绍一下 lisp 符号数据类型:
- 符号是一种通过地址管理字符串的数据。
- 符号可以被快速地索引、比较。
- 作为基本数据类型之一,你可以用
(symbol? id)来判断一个 id 是否为符号。
使用方式很简单,(quote datum) 或者用一种快捷的写法 'datum:
(quote foo) ; => 'foo
(quote (1 2 3 4)) ; => '(1 2 3 4),即一个链表
(quote (1 . 2)) ; => '(1 . 2),即一个序对
'(list 1 jdf hepp) ; => '(list 1 jdf hepp),同 (quote (list 1 jdf hepp))我们首先来模拟一个 REPL:
(define repl
(λ ()
(display "REPL⇒")
(let ([exp (read)]) ; (read) 将读取我们接下来要输入的字符串
; 在遇到 LF 或 CR/LF 后会返回转换后的 symbol
(cond
[(equal? exp '(exit)) "exit"] ; 退出条件
[else
(displayln (calculator exp)) ; 打印并换行
(repl)])))) ; 继续读取下一次输入我们在 REPL 中输入 "(+ 1 2)" 时,(read) 将会返回一个填充物为 '(+ 1 2) 的链表。
既然 (read) 已经将数据直接转换好了,那我们只需要关心怎么样使这些数据起作用就行了。
对符号的解释
当遍历到一个合法的符号时(+-×÷),希望能够得到相对应的过程(函数)。直接判断就行了:
(define find-op
(λ (op)
(cond
[(eq? '+ op) +]
[(eq? '- op) -]
[(eq? '* op) ×] ; REPL 那个小输入框用不了 Tex 。。。
[(eq? '/ op) ÷]))) ; 同上树遍历
我们计算器的语法实在太简单,它的数据结构就如上面那张图的数据结构一样。 因此这个计算器的算法,实际上就是在这棵树上的一种遍历操作。
当使用 '(+ 1 (- 1 2) 3) 调用 car 时我们可以得到 +,下一次遍历时可以得到 1,
再下一次会得到 (- 1 2)。到了最后只剩下一个 '() 时再调用 car 则会出错,
也就是返回值的多元性使得我们必须要对每一个节点彻底求值:
(define calc
(λ (exp)
(cond
[(null? exp) null] ; ➀ 已经没有数据可以遍历了
[(number? exp) exp] ; ➁ 直接返回这个数字
[else
(let ([e1 (car exp)]
[e2 (cdr exp)])
(cond
[(symbol? e1) ; ➂ 如果是一个符号
(cond
[(eq? '+ e1) (apply + (calc e2))] ; apply 这个匹配的函数
[(eq? '- e1) (apply - (calc e2))]
[(eq? '* e1) (apply × (calc e2))]
[(eq? '/ e1) (apply ÷ (calc e2))])]
[else
(cons (calc2 e1) (calc2 e2))]))]))) ; e1 和 e2 不一定是数字
; 如果是数字将会在 ➁ 中返回
; 如果是S表达式会在 ➂ 被计算
; 没有元素时会 cons '() 成为链表apply 是个神奇的函数,把多个参数放到链表中去 apply 一个函数时,相当于用多个参数去调用这个函数。
如果这个函数接受的参数形式刚好还是以序对的形式则会发生一些奇特的现象:
> (apply + '(1 2 3))
6
> (apply + 1 2 '(3))
6
> (apply + '())
0
> (apply map `(,(λ (x) (+ x 1)) (1 2 3)))
'(2 3 4)
> (apply sort `('(2 1) ,<))
'(1 2)模式匹配
上面的计算器可以通过模式匹配实现更加简便的写法:
(define calc
(λ (exp)
(match exp
[(? null? x) x]
[(? number? x) x]
[(list (? symbol? op) e ...)
(match op
['+ (apply + (calc e))]
['- (apply - (calc e))]
['* (apply × (calc e))]
['/ (apply ÷ (calc e))])]
[(list e1 e2 ...)
(cons (calc e1) (calc e2))])))完
以上就是全部内容,下次可能会写一些变量函数之类的东西。
不过就这一篇我都写了快 1 个星期了。。。
顺便春节快乐。