区块链领域都曾流行过哪些算法和数据结构

Jul 14, 2018 PATRICIA merkle-tree blockchain data-struct information-retrieval

区块链已越来越嵌入到我们的日常生活，这也算是一种大势所趋了。在数据体量越来越庞大的趋势下，对数据筛选和信息检索的相关知识也越来越下沉到每一个普通的开发仔，于是我也想来写文章介绍一下区块链领域中那些耳熟能详的算法。

本文主讲数据结构和算法，那么就有必要先给这些数据结构和算法之间的关系下一些定义： 「给算法的数据规划一种出合理的结构，尽可能使该数据在数学上天生拥有一些能够便于该算法操作的性质」。



Patricia Trie

PATRICIA: Practical Algorithm To Retrieve Information Coded In Alphanumeric.

Patricia Trie 是 Trie 的一个进化变种，它在字符串子串匹配上有着非常优异的表现， 这使得 Patricia 作为一种高效的全文检索算法一度声名大噪，并且在自然语言处理领域也有相当广泛的应用。

Patricia Trie 每个节点有且仅有一个「位索引值」指示整串字节流中每处产生差异的位置， 然后只要将需要匹配的文本转换成字节流，再根据位索引值选择分支即可。

假如有以下的由字节流与字符串的组成的映射：


0111 0011  0110 1101  0110 1001  0110 1100  0110 0101  0000 0000  0000 0000 : smile
0111 0011  0110 1101  0110 1001  0110 1100  0110 0101  0110 0100  0000 0000 : smiled
0111 0011  0110 1101  0110 1001  0110 1100  0110 0101  0111 0011  0000 0000 : smiles
0111 0011  0110 1101  0110 1001  0110 1100  0110 1001  0110 1110  0110 0111 : smiling

产生差异的位均已加粗标明，这些位置都将产生一个分岔的节点，而该位置的下标将成为对应节点的位索引值。

这些键所组成的 Patricia Trie 看起来会是这样的：

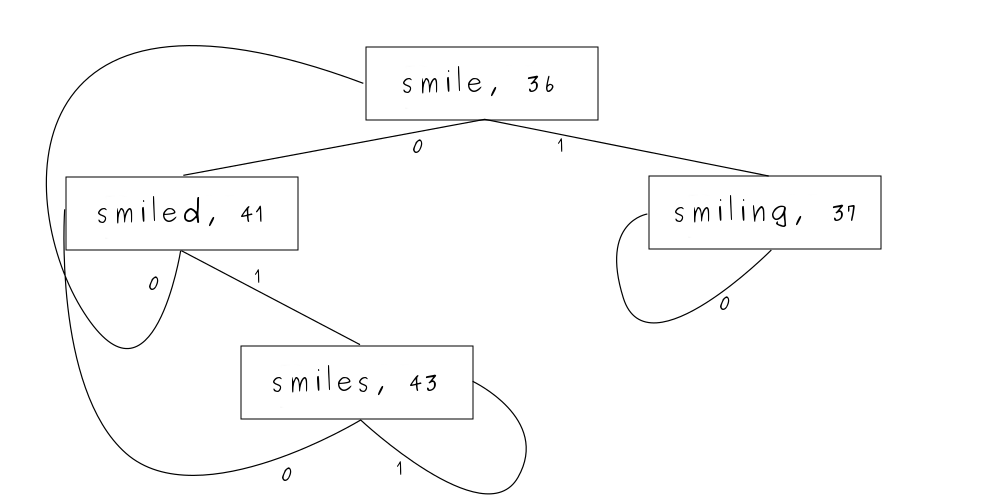
PAT Trie

!TODO_1 这图我画得不好，所有字符串单开一个节点存值看起来会更加直观。

!TODO_2 有时间我会将下面所有 png 格时地图片都用 TikZ 重画一遍。

Patricia Trie 查找的时间复杂度和树的深度相关。由于树的构造取决于 0, 1 的分布，最坏情况下是单支树， 此时时间复杂度达到 $\Omicron(n)$，最好情况下是平衡二叉树，时间复杂度为 $\Omicron(\log(n))$， 因此整体上看也是一种二叉搜索树，但作为压缩的二叉查找树，其存储的空间代价大大减少了。



Merkle Tree

Merkle Tree 的应用领域相当广泛，随着互联网的出现，需要对数据进行完整性效验的领域也应运蓬勃发展， Merkle Tree 就是在这种环境下能够高效完成效验工作同时还能精确定位到损坏的数据，最终赢得了大家的青睐。

特征 & 结构

Merkle Tree 一般是二叉树，也可以多叉树。

非叶子节点的 hash 值根据所有子节点的 hash 值通过相同的算法计算得出：

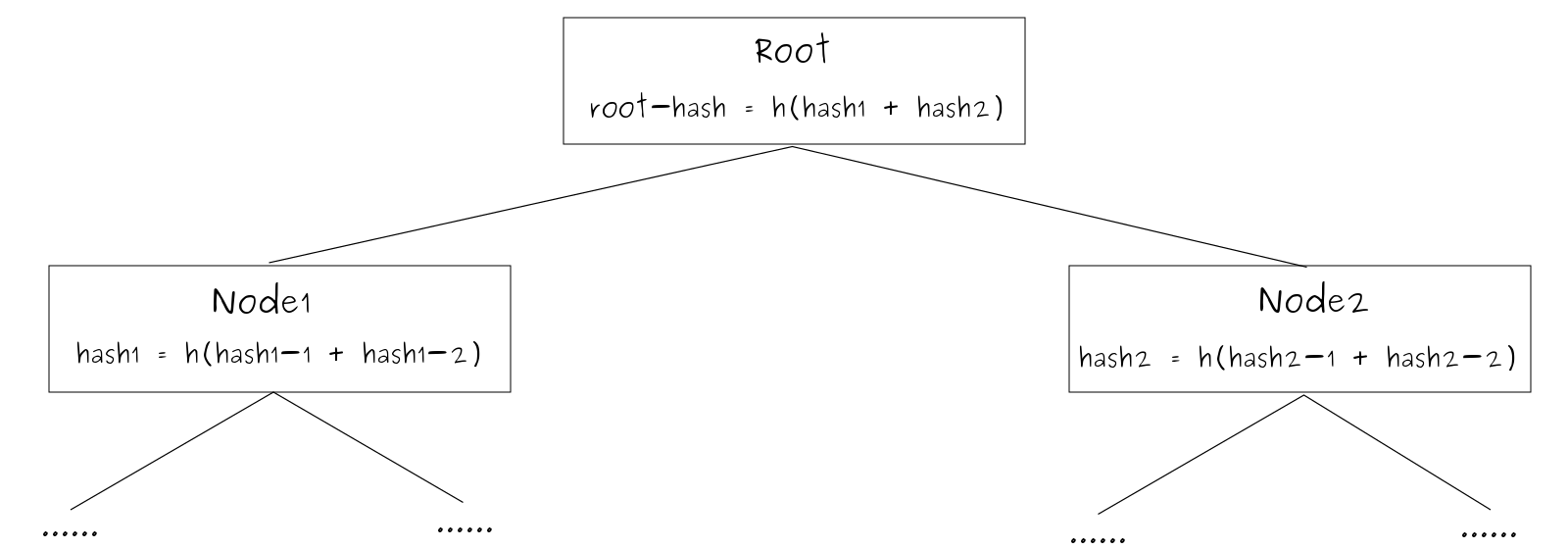
Merkle Tree 1

叶子节点的 hash 值是某份数据的 hash 值：

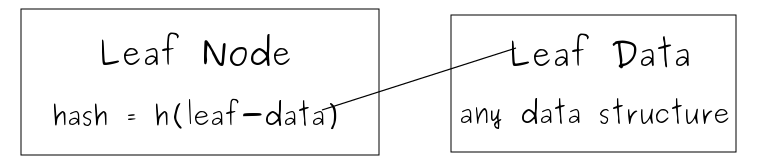
Merkle Tree 2

Hash

Merkle Tree 通常也被称作 Hash Tree，由于对数据的同余操作是一项非常频繁的操作， 对于较大的数据块而言，使用 hash 值代替数据块本身进行比较已是一种不成文的规矩。 比如 Java 中的对象都会继承两个来自 Object 的方法：hashCode(), equals(obj)。

Hash 尽管能够帮助计算机快速进行比较，但当要比较对象的是两组具有堆叠结构的数组时， 比如是两个文件夹，文件夹中还有文件夹，如何快速比较两个文件夹中的数据？ 在文件传输时，为了支持断点传输，文件一般会被切割为固定大小的多个片段， 如何快速对下载的文件进行完整性验证，并快速定位到具体损坏的部分？

数据校验

为了方便起见这里用 VCS 来举个简单的例子来展示 Merkle Tree 在校验数据时的一般过程： 现在某个 git 仓库的某个文件夹中共包含了 8 个文件，这个文件夹的 Merkle Tree 可能是这个样子的：

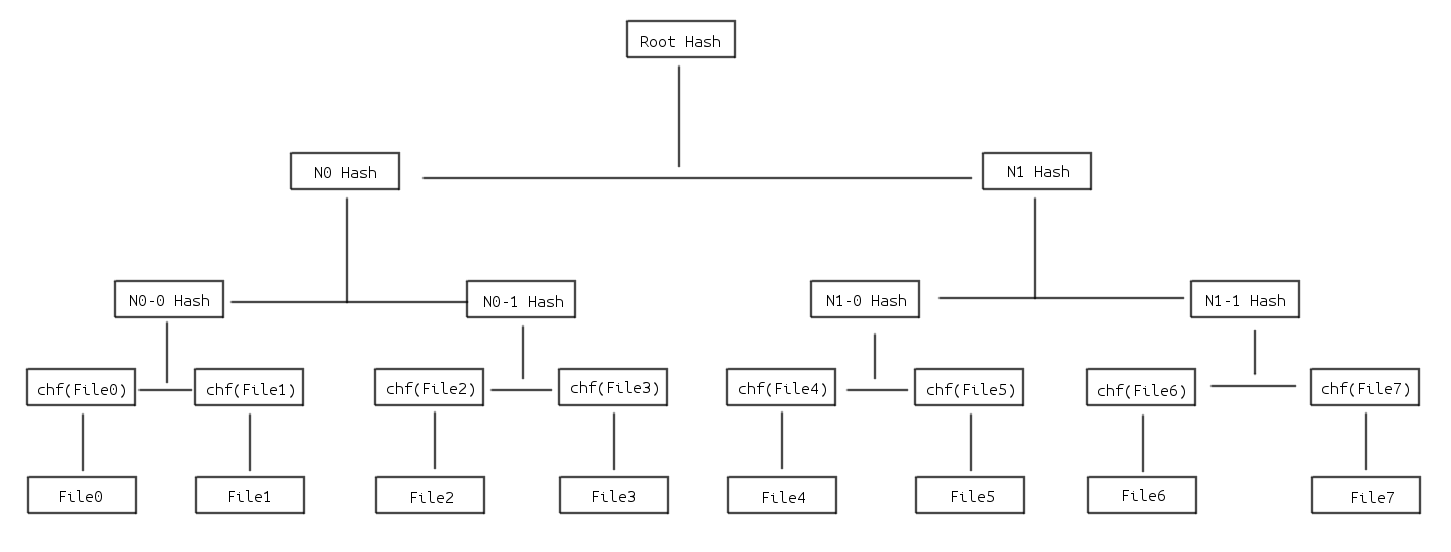
Merkle Tree 2

chf 为这里的哈希函数，这里用二叉树作为例子，但实际上也有可能是多叉树。这时当修改了其中的 File2 时：

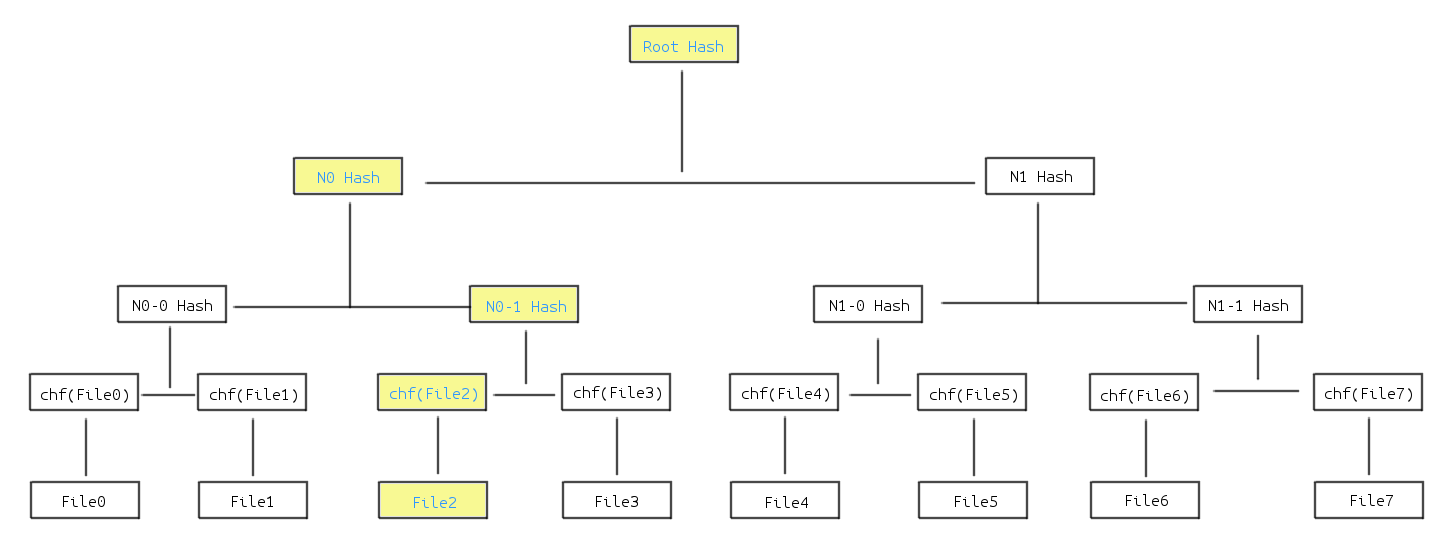
Merkle Tree 2

可以看到由于 File2 的 hash 值被改变从而导致与 File2 相关的所有分支的 hash 也发生了改变。 这时只要从 roothash 开始逐一与原来的 hash 值进行比较，就可以一路追溯到某个叶子。 这也是输入 git status 时背后的一般工作原理。

当输入 git diff 时也是差不多的原理，只不过比较的对象具体到了组成其的字节流：

  • 对于整个文件的完整字节，可以将一个段落的字节当作叶子。
  • 对于段落，可以用标点符号或空格等继续细分成单词或字母。

树的节点越密集，越能够突出具体的细节。

说到 Git，就不得不提一下它使用的一种叫 Merkle DAG 的结构， Merkle DAG 实际上也在 IPFS 以及区块链应用中得到广泛应用。

Merkle Tree 2

IPFS 则是一种支持在 P2P 环境中寻址的互联网传输方案，同时也是一种内容可寻址的对等超媒体分发协议。 其概念大致可以概括为内容可寻址，版本化，点对点超媒体的分布式存储，传输。

如果说基于 TCP 的网络传输是通过域名建立起 C/S 的模型，通过路径使用请求、应答的方式进行传输的话； 那么 IPFS 就相当于大家共处一个 P2P 的网络集群环境中，依靠唯一的 hash 值在 Merkle DAG 中展开索引， 并在随机分布的节点群中随机地获取数据包，最终拼凑成一个完整的数据。

不足之处

Merkle Tree 并不完美，这点可以在 Merkle Tree 增删改查操作的复杂度上得到体现：

  • Merkle Tree 进行数据校验的时空复杂度均为 $\Omicron(\log(n))$，这里指比较的次数。
  • 生成一棵 Merkle Tree 的空间复杂度仅 $\Omicron(\log(n))$，这里指树的高度。 而时间复杂度达到 $\Omicron(n\log(n))$，这里指 chf 的执行次数，包括了叶子节点和所有中间节点。

Merkle Tree 叶子数据的更新总是意味着与该叶子节点相关的所有父节点其 hash 值也需要得到更新：

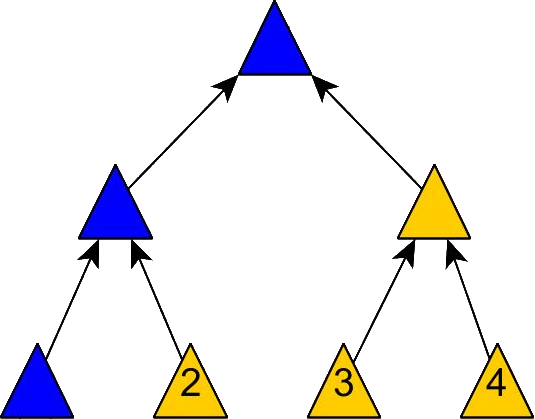
Merkle Tree 2

更新并不会对 Merkle Tree 的结构造成影响，时间复杂度为 $\Omicron(\log(n))$， 但插入和删除会改变 Merkle Tree 的结构，如果现在插入一个新块 data0：

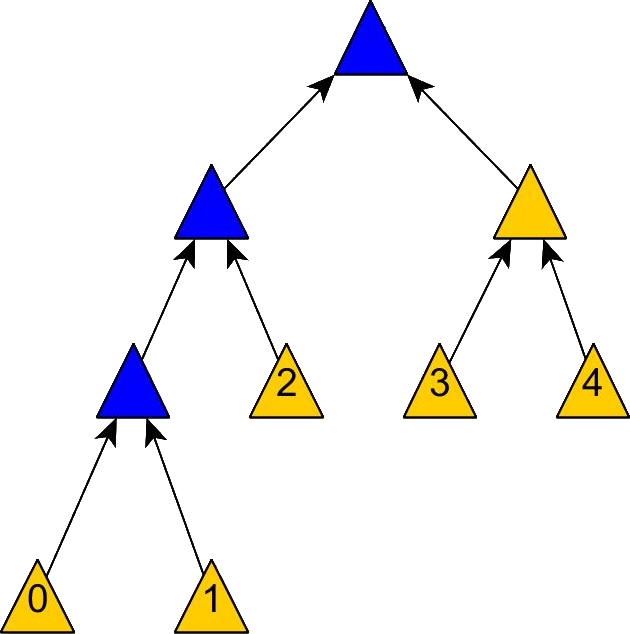
Merkle Tree 2

像这样直接插入一个块直觉上所需复杂度仍是 $\Omicron(\log(n))$，但考虑如果需要满足以下条件：

  • Merkle Tree 在更新叶子数据需要 re-hash 的时间复杂度控制在 $\Omicron(\log(n))$ 以内。
  • Merkle Tree 对数据校验的时间复杂度控制在 $\Omicron(\log(n))$ 以内。
  • 除非原始 Merkle Tree 的 $n \equiv 0 \mod{2}$，否则插入数据后的 Merkle Tree 没有孤块。
  • 插入后的 Merkle Tree 保持平衡，数据之间的顺序保持一致。

所以插入后的 Merkle Tree 应该是这样的：

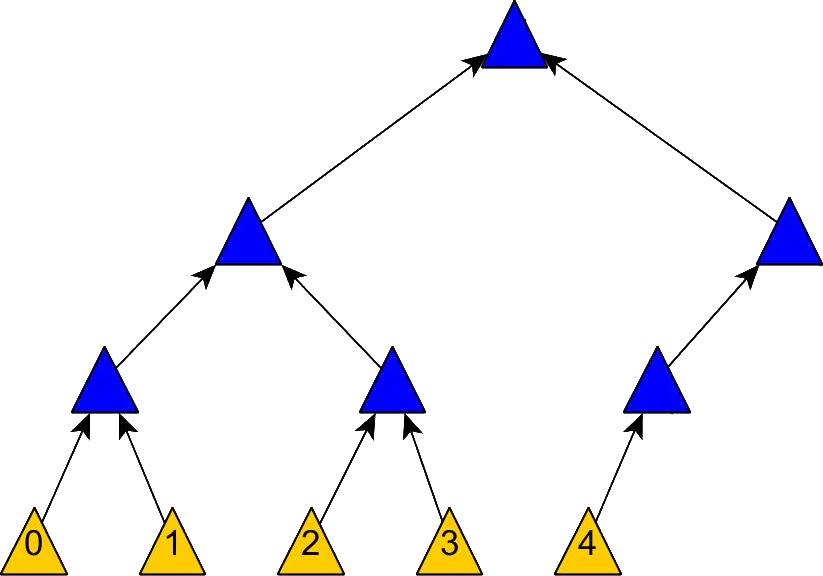
Merkle Tree 2

插入后的 Merkle Tree 保持了良好的平衡性，但代价却是需要重新构建一棵完整 Merkle Tree。 对于 Merkle Tree 的插入和删除实际上是一个工程问题，对于不同的需求在实现上可能会有不同的妥协。



Merkle Patricia Tree

Merkle Patricia Trie，顾名思义，即符合 PATRICIA 性质的 Merkle Tree，以下简称 MPT。 MPT 随着区块链应用的热点而被大众所熟知，那么这种数据结构的好处又是什么？

MPT 提供了一个基于加密学的、自校验防篡改的数据结构用来存储键值对关系。 在多数规范中键值的类型都只限定成字节流，并且修改后的 MPT 是确定的。

站在区块链的角度来看，一笔交易被执行以后就已经是不可逆的，储存着交易的树一旦生成， 此时关于树的增删改操作都是无意义的，唯一有意义的操作只有交易关于正确性及完整性的效验。 而用作储存交易信息的数据结构， Merkle Tree 无疑是最合适的选择。

虽然所有的交易和收据都能采用 Merkle Tree 作为数据结构，但区块链中不止储存着交易，还有状态。 状态树的叶子由一串 20 字节的地址映射到一个叫 Account 的对象，而 Account 的数据是可能频繁修改的。 状态树可能需要频繁地处理写操作：balance 和 nonce 经常需要更新，Account 也会经常执行插入和删除。

来看一个例子，不考虑状态树结构上隐含的映射与加密，该状态树的结构是这样的：

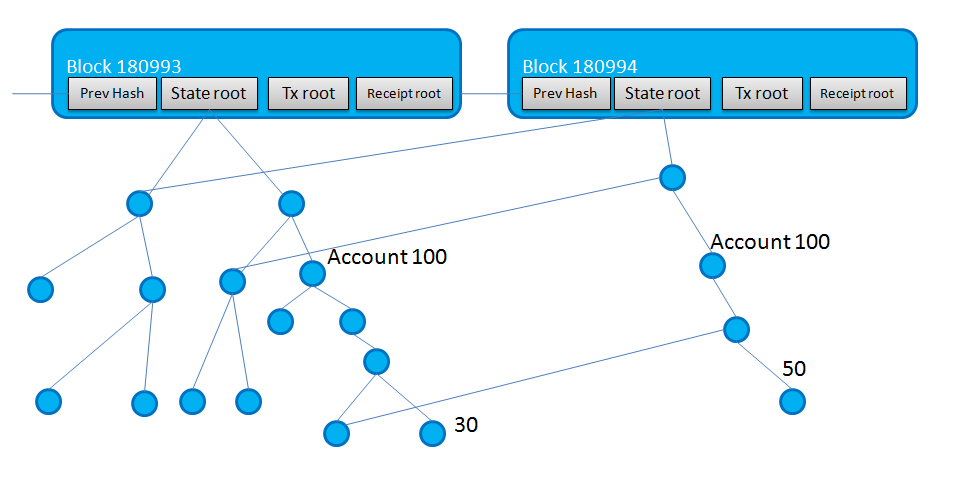
Merkle Tree 2

除了 Account100 右子节点下的一个叶子节点的数据从 30 修改为 50，树的其余部分完全一致。

此时就需要这样一种数据结构，它能在一次增删改操作中保留原结构的特性同时避免重复计算整棵树的 hash。 这种数据结构同样得包括两个非常好的第二特征：

  • 树的深度是有限制的，不然，攻击者可以通过操纵树的深度，使得区块更新变得极其缓慢。
  • roothash 和叶子的排列顺序无关，对树操作的顺序不会影响树的结构，即满足阿贝尔群。

显然，Trie 是最能够同时满足上面的性质的的结构，而为了能够更高效地运作，MPT 便是最佳的数据结构。

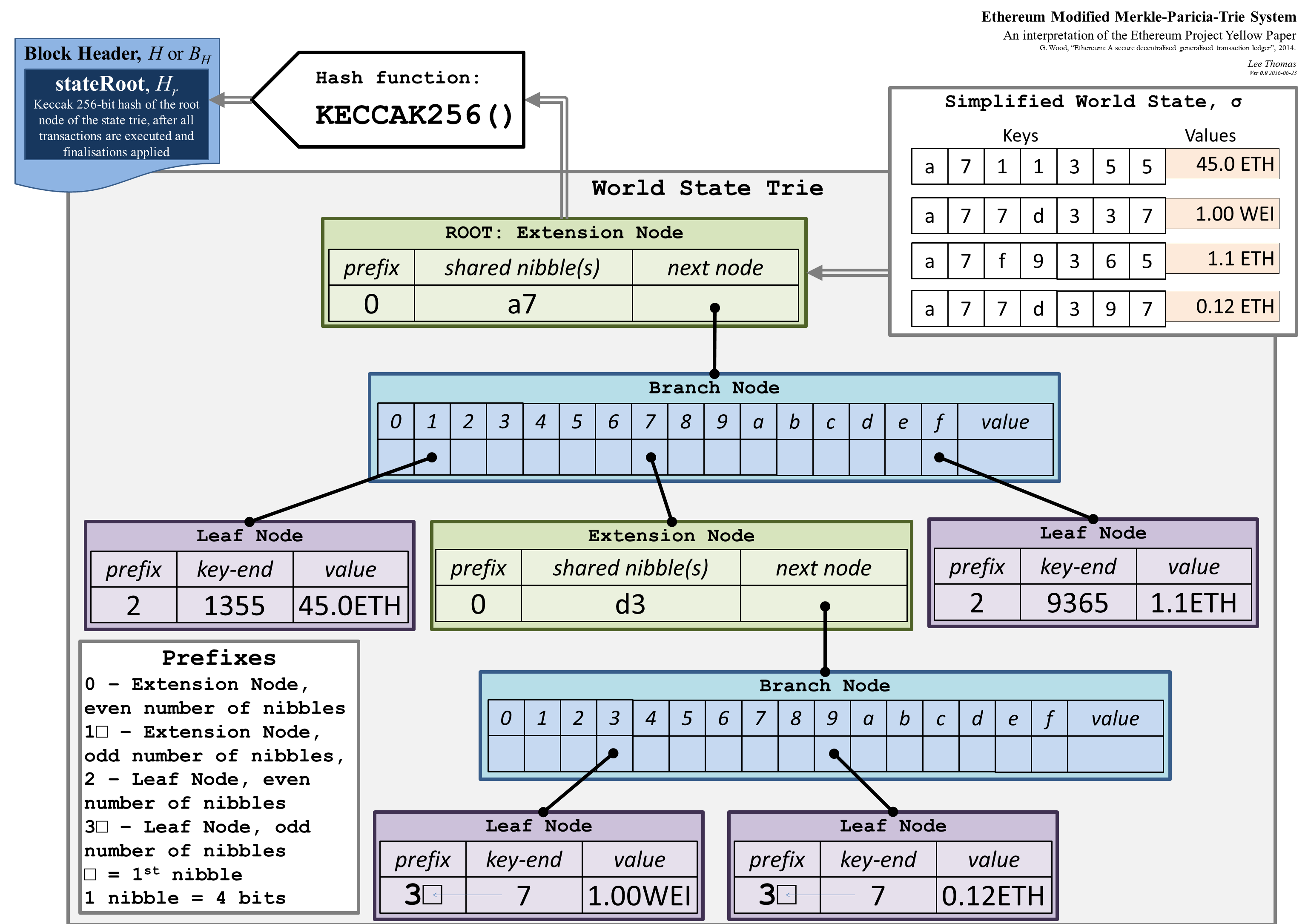
除此以外，以太坊使用的 MPT 还是一种带类型的 MPT，它的节点按功能和存储数据的类型分为 4 种：

  • null := KECCAK256(nil)
  • extension : [nibble, next]
    nibble 为完整 hash 中的一个切片、共享的一段序列，可以理解为传统 PATRICIA 节点。
    next 可能指向了下一个节点，也可能指向了一个值。
  • branch : [v0 ... v15, value]
    vn 为单个 16 进制字符，传统 PATRICIA 用 0 和 1 形成二叉树，而 branch 允许达到 16 个 分支。
    value 是使 20 和 36 字节的字节流能够储存在同一树上的兼容，使 branch 同时拥有 leaf 的功能。
  • leaf : [key-end, value]
    key-end 为补位，因为完整的 hash 长度需要达到 20 或 32 字节。

m-mpt



DHT Distribution Hash Table

!TODO : p2p 下 BT 技术如何使用 patricia 计算距离？？？ IPFS 和 DHT 的关系？？

つづく